深度优先搜索（dfs）-津桥芝士平台

深度优先搜索是一种遍历的方式，同时也是连接dp（动态规划）的桥梁

举个例子：

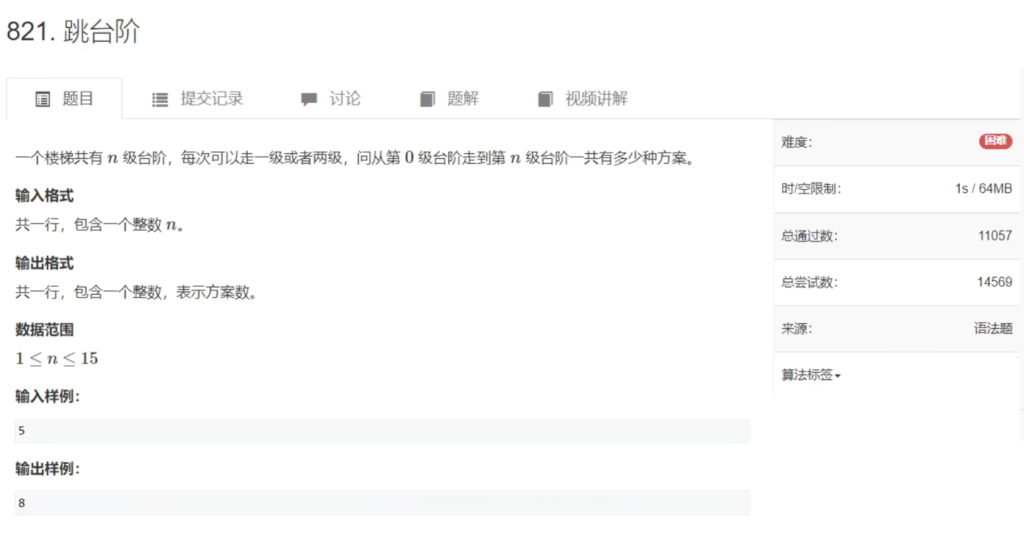
这是dfs和dp很经典的列题，为什么即是dfs也是dp，请看接下来题解

dfs解法（注：需要有一定递归基础）

#include <iostream>
int n,cnt=0;
void dfs(int x)
{
	if (x == n) {  //判断是否达到条件
		cnt++;
		return;
	}
	else if (x > n) {  //若遍历的超出所给台阶数则直接返回不算次数
		return;
	}
	//选择跳一个台阶
	x += 1;
	dfs(x);
	x -= 1; //回溯
	//选择跳两个台阶
	x += 2;
	dfs(x);
	x -= 2; //回溯
}
int main()
{
	std::cin >> n;
	dfs(0);		//深度优先搜索总数从0开始
	std::cout << cnt << "\n";
	return 0;
}

dp写法（注：dp难度极大无固定模板，每题解决方法都不同）

思路：若n为1 则有1种 1

若n为2 则有2种 1 1 或 2

若n为3 则有3种 1 1 1 或1 2 或2 1

若n为4 则有5种（太多懒得写）不难发现当n>=3时，an=a(n-1)+a(n-2);

则发现的此题的转换方程an=a(n-1)+a(n-2);

代码如下

#include <iostream>
int main()
{
	int a[10000];
	std::cin >> n;
	a[1] = 1, a[2] = 2;
	for (int i = 3; i <= n; i++) {
		a[i] = a[i - 1] + a[i - 2];
	}
	std::cout << a[n] << "\n";
	return 0;
}

会发现dp相比dfs代码量减少的同时更高效；

版权声明 1 本网站名称：津桥芝士站
2 本站永久网址： https://wang-sz.cn/
3 本网站的文章部分内容可能来源于网络，仅供大家学习与参考，如有侵权，请联系站长进行删除处理。
4 本站一切资源不代表本站立场，并不代表本站赞同其观点和对其真实性负责。
5 本站一律禁止以任何方式发布或转载任何违法的相关信息，访客发现请向站长举报
6 本站资源大多存储在云盘，如发现链接失效，请联系我们我们会第一时间更新。
7 本站采用知识共享署名-非商业性使用-相同方式共享4.0国际许可协议进行许可

THE END

C++C语言数据结构数据结构与算法算法
# 深度优先搜索（dfs）